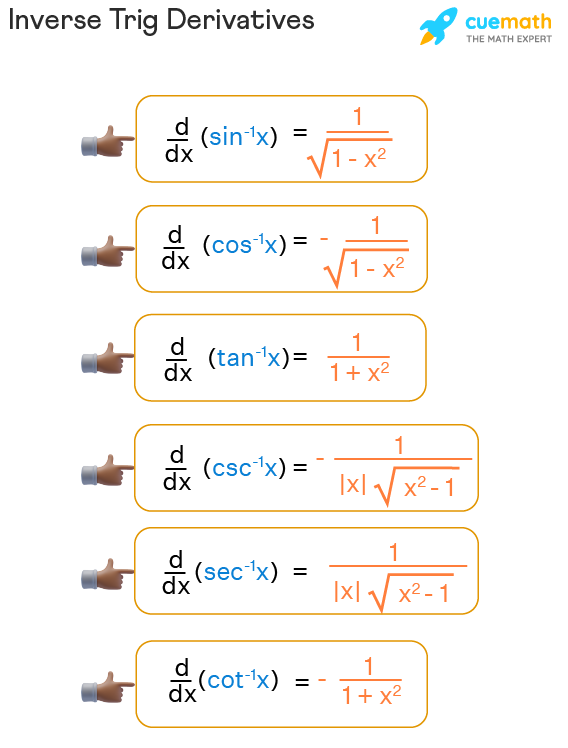
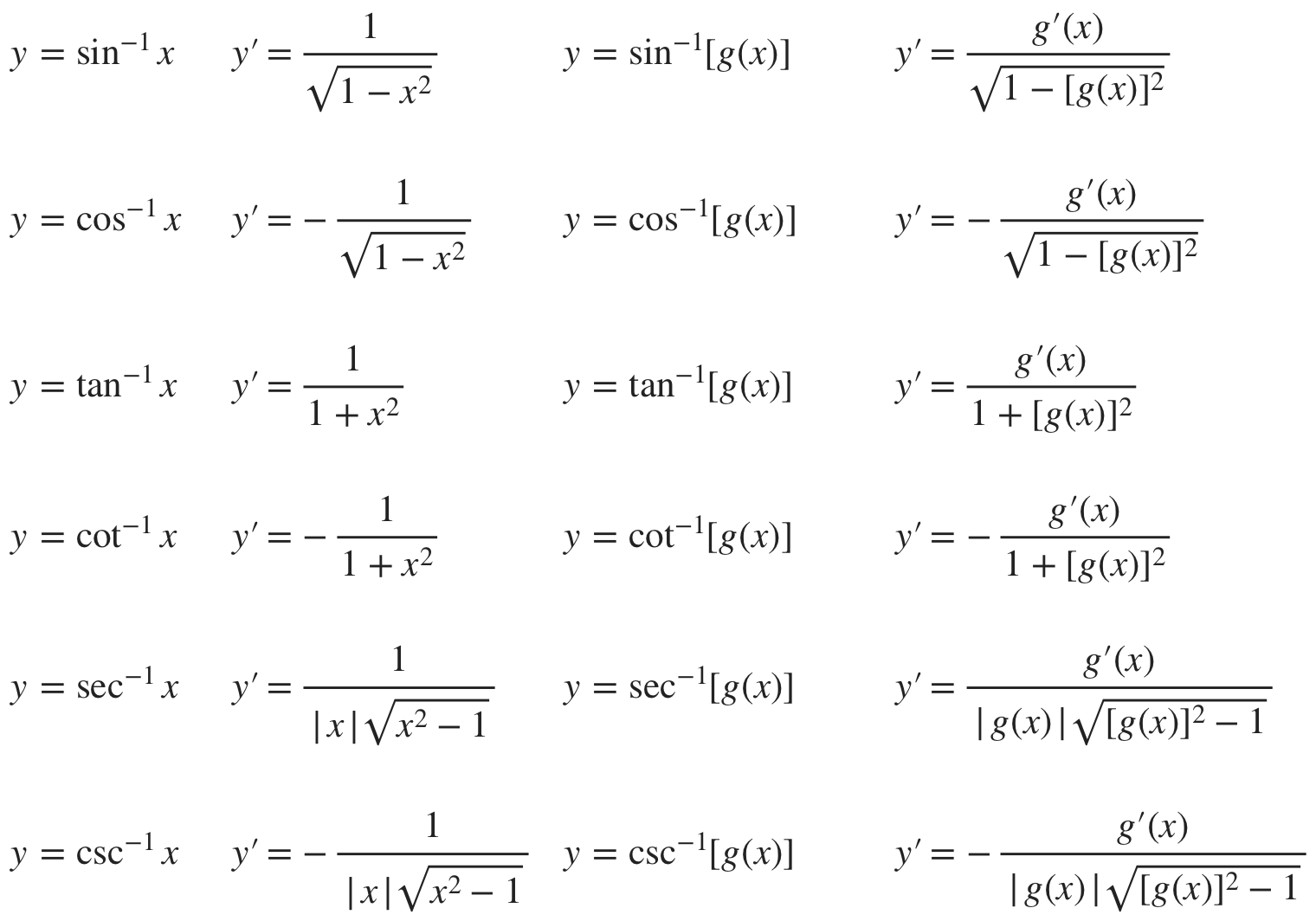Derivatives Of Trig Functions Cheat Sheet
Derivatives Of Trig Functions Cheat Sheet - Sum difference rule \left (f\pm. N (x)dx (a) if the 2power n of cosine is odd (n =2k + 1), save one cosine factor and use cos (x)=1 sin: \tan (x) = \frac {\sin (x)} {\cos (x)} \tan (x) = \frac {1} {\cot (x)} \cot (x) = \frac {1} {\tan (x)} \cot (x) = \frac {\cos. (fg)0 = f0g +fg0 4. Where c is a constant 2. Web derivatives cheat sheet derivative rules 1. D dx (c) = 0; D dx (xn) = nxn 1 3. F g 0 = f0g 0fg g2 5. Web trigonometric derivatives and integrals:
D dx (c) = 0; Where c is a constant 2. \tan (x) = \frac {\sin (x)} {\cos (x)} \tan (x) = \frac {1} {\cot (x)} \cot (x) = \frac {1} {\tan (x)} \cot (x) = \frac {\cos. R strategy for evaluating sin: F g 0 = f0g 0fg g2 5. Web trigonometric derivatives and integrals: N (x)dx (a) if the 2power n of cosine is odd (n =2k + 1), save one cosine factor and use cos (x)=1 sin: Sum difference rule \left (f\pm. (fg)0 = f0g +fg0 4. Web derivatives cheat sheet derivative rules 1.
Web trigonometric derivatives and integrals: Sum difference rule \left (f\pm. Web derivatives cheat sheet derivative rules 1. N (x)dx (a) if the 2power n of cosine is odd (n =2k + 1), save one cosine factor and use cos (x)=1 sin: R strategy for evaluating sin: (fg)0 = f0g +fg0 4. \tan (x) = \frac {\sin (x)} {\cos (x)} \tan (x) = \frac {1} {\cot (x)} \cot (x) = \frac {1} {\tan (x)} \cot (x) = \frac {\cos. F g 0 = f0g 0fg g2 5. Where c is a constant 2. D dx (xn) = nxn 1 3.
Integral Cheat Sheet Calculus derivative calc trig hyperbolic integral
F g 0 = f0g 0fg g2 5. N (x)dx (a) if the 2power n of cosine is odd (n =2k + 1), save one cosine factor and use cos (x)=1 sin: Sum difference rule \left (f\pm. R strategy for evaluating sin: Web derivatives cheat sheet derivative rules 1.
Pin on Math cheat sheet
R strategy for evaluating sin: Web derivatives cheat sheet derivative rules 1. (fg)0 = f0g +fg0 4. D dx (c) = 0; F g 0 = f0g 0fg g2 5.
Derivatives of inverse trig functions Studying math, Physics and
Where c is a constant 2. F g 0 = f0g 0fg g2 5. R strategy for evaluating sin: Web trigonometric derivatives and integrals: \tan (x) = \frac {\sin (x)} {\cos (x)} \tan (x) = \frac {1} {\cot (x)} \cot (x) = \frac {1} {\tan (x)} \cot (x) = \frac {\cos.
Trig cheat sheet linkjolo
Web derivatives cheat sheet derivative rules 1. Where c is a constant 2. \tan (x) = \frac {\sin (x)} {\cos (x)} \tan (x) = \frac {1} {\cot (x)} \cot (x) = \frac {1} {\tan (x)} \cot (x) = \frac {\cos. D dx (c) = 0; Web trigonometric derivatives and integrals:
Derivatives Cheat Sheet PDF
N (x)dx (a) if the 2power n of cosine is odd (n =2k + 1), save one cosine factor and use cos (x)=1 sin: D dx (xn) = nxn 1 3. Web derivatives cheat sheet derivative rules 1. F g 0 = f0g 0fg g2 5. R strategy for evaluating sin:
Trigonometry Laws and Identities Studying math, Math methods
R strategy for evaluating sin: (fg)0 = f0g +fg0 4. Web derivatives cheat sheet derivative rules 1. \tan (x) = \frac {\sin (x)} {\cos (x)} \tan (x) = \frac {1} {\cot (x)} \cot (x) = \frac {1} {\tan (x)} \cot (x) = \frac {\cos. Sum difference rule \left (f\pm.
Trig Cheat Sheet 1.4 PDF Trigonometric Functions Sine
(fg)0 = f0g +fg0 4. D dx (xn) = nxn 1 3. F g 0 = f0g 0fg g2 5. N (x)dx (a) if the 2power n of cosine is odd (n =2k + 1), save one cosine factor and use cos (x)=1 sin: Web trigonometric derivatives and integrals:
Finding inverse trig derivatives — Krista King Math Online math help
Where c is a constant 2. D dx (c) = 0; F g 0 = f0g 0fg g2 5. Web trigonometric derivatives and integrals: Web derivatives cheat sheet derivative rules 1.
Inverse Trig Derivatives (Derivatives of Inverse Trig Functions)
Web derivatives cheat sheet derivative rules 1. D dx (xn) = nxn 1 3. F g 0 = f0g 0fg g2 5. Where c is a constant 2. \tan (x) = \frac {\sin (x)} {\cos (x)} \tan (x) = \frac {1} {\cot (x)} \cot (x) = \frac {1} {\tan (x)} \cot (x) = \frac {\cos.
(PDF) Trig Cheat Sheet Jerome Delen Academia.edu
F g 0 = f0g 0fg g2 5. Where c is a constant 2. N (x)dx (a) if the 2power n of cosine is odd (n =2k + 1), save one cosine factor and use cos (x)=1 sin: Web derivatives cheat sheet derivative rules 1. D dx (xn) = nxn 1 3.
Sum Difference Rule \Left (F\Pm.
Web trigonometric derivatives and integrals: D dx (c) = 0; \tan (x) = \frac {\sin (x)} {\cos (x)} \tan (x) = \frac {1} {\cot (x)} \cot (x) = \frac {1} {\tan (x)} \cot (x) = \frac {\cos. N (x)dx (a) if the 2power n of cosine is odd (n =2k + 1), save one cosine factor and use cos (x)=1 sin:
Web Derivatives Cheat Sheet Derivative Rules 1.
Where c is a constant 2. (fg)0 = f0g +fg0 4. F g 0 = f0g 0fg g2 5. R strategy for evaluating sin: