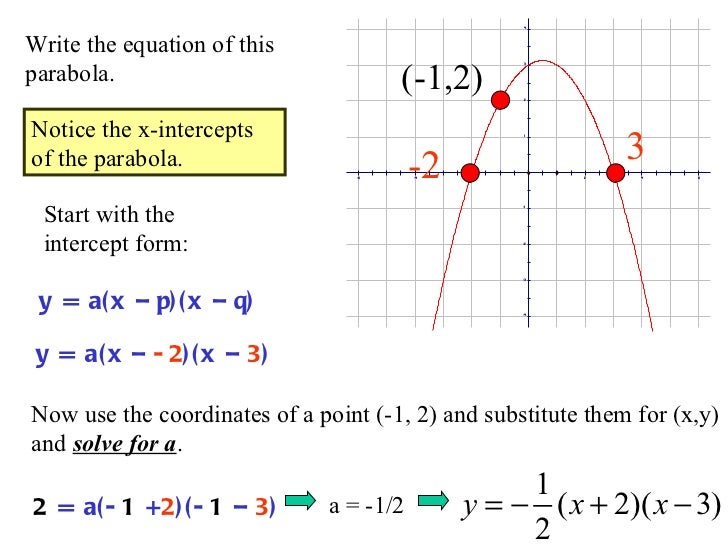
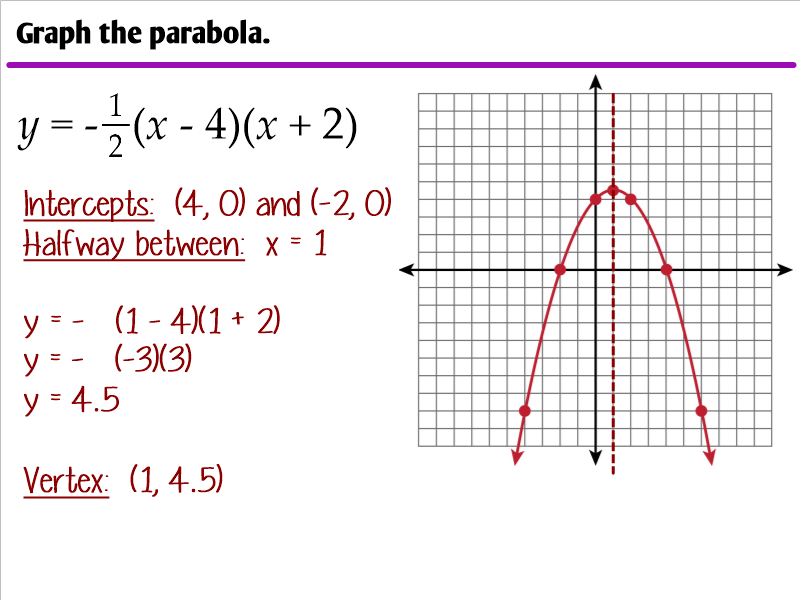
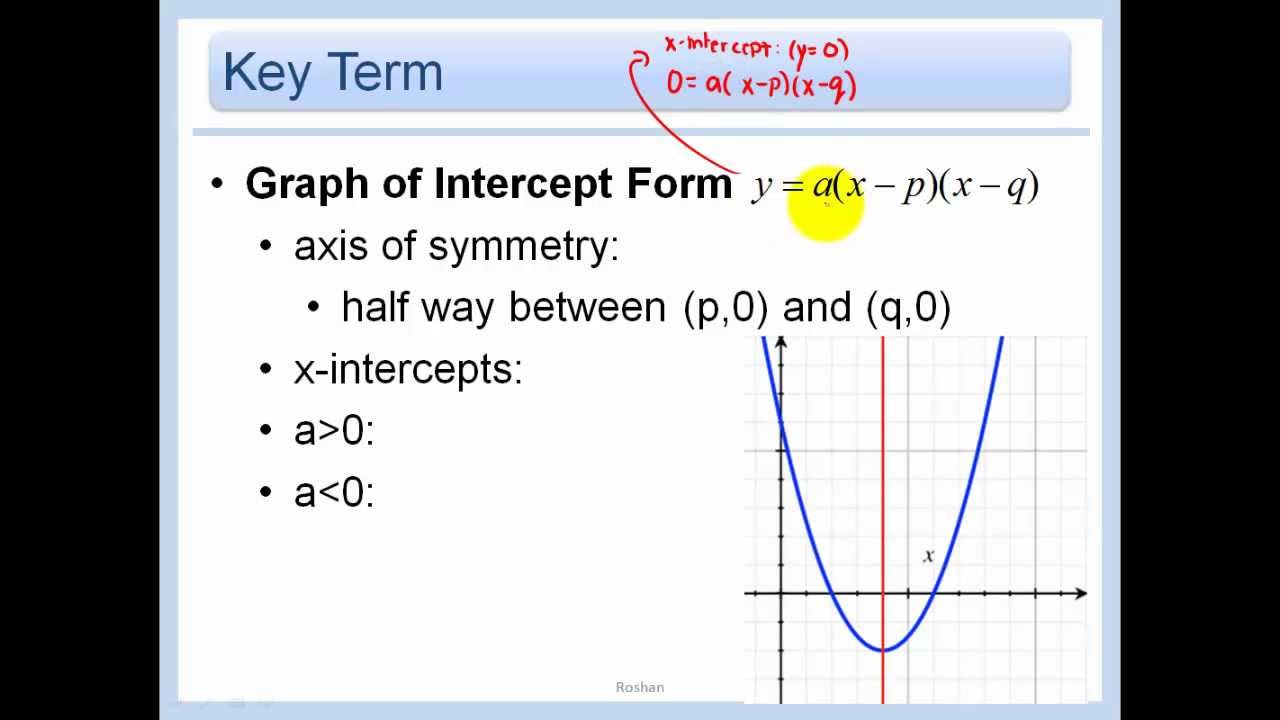
Parabola Intercept Form
Parabola Intercept Form - (x − h)2 = 4p(y − k) a parabola is defined as the locus (or collection) of points equidistant from a given point (the focus) and a given line (the directrix). The intercept of a quadratic function is the point where the function’s graph intersects or crosses an axis. Web explore different kinds of parabolas, and learn about the standard form, the intercept form, and the vertex form of parabola equations. So, plug in zero for x and solve for y: There are three main forms of linear equations. Given a quadratic function in general form, find the vertex. Y = 12 x2 + 48 x + 49. The axis of symmetry lies halfway between these points, at x = 0.5. Notice that in this form, it is much more tedious to find various characteristics of the parabola than it is given the standard form of a parabola in the section above. The only value that is relatively easy to determine is the vertex when using vertex form.
It fits several superficially different mathematical descriptions, which can all be proved to define exactly the same curves. So, plug in zero for x and solve for y: Web how to graph a parabola when it is in intercept form. Y = 12 x2 + 48 x + 49. Given a quadratic function in general form, find the vertex. We review all three in this article. We will be finding the zeros and vertex points to graph the quadratic. Vertex form provides a vertex at (h,k). There are three main forms of linear equations. (x − h)2 = 4p(y − k) a parabola is defined as the locus (or collection) of points equidistant from a given point (the focus) and a given line (the directrix).
Find the equation of the line in all three forms listed above. One of the simplest of these forms is: We review all three in this article. Web how to graph a parabola when it is in intercept form. It fits several superficially different mathematical descriptions, which can all be proved to define exactly the same curves. Web #quadraticequation #parabola #quadratic this video shows how to write a quadratic equation for a given graph of a parabola in intercept form.a similar video. Identify a quadratic function written in general and vertex form. (x − h)2 = 4p(y − k) a parabola is defined as the locus (or collection) of points equidistant from a given point (the focus) and a given line (the directrix). Web a parabola comes from three forms of a quadratic: We will be finding the zeros and vertex points to graph the quadratic.
Quadratic Equation X Intercept Formula Tessshebaylo
Web explore different kinds of parabolas, and learn about the standard form, the intercept form, and the vertex form of parabola equations. One of the simplest of these forms is: The only value that is relatively easy to determine is the vertex when using vertex form. And the form that it's in, it's in factored form already, it makes it.
Parabolas in Standard, Intercept, and Vertex Form Video & Lesson
X = ay 2 + by + c vertex form: It fits several superficially different mathematical descriptions, which can all be proved to define exactly the same curves. Vertex, standard and intercept form. (x − h)2 = 4p(y − k) a parabola is defined as the locus (or collection) of points equidistant from a given point (the focus) and a.
cribsheets — Matthew Handy Maths + Physics tutor in Harrogate
It fits several superficially different mathematical descriptions, which can all be proved to define exactly the same curves. Characteristics of the graph of y = a(x— + k:. Web #quadraticequation #parabola #quadratic this video shows how to write a quadratic equation for a given graph of a parabola in intercept form.a similar video. The only value that is relatively easy.
Parabola Intercept form graphing YouTube
We review all three in this article. X = ay 2 + by + c vertex form: Web how to graph a parabola when it is in intercept form. Example 1 identifying the characteristics of a parabola Notice that in this form, it is much more tedious to find various characteristics of the parabola than it is given the standard.
4.3 Graphing Parabolas in Intercept Form Ms. Zeilstra's Math Classes
The equation of a left/right opened parabola can be in one of the following three forms: Web we are graphing a quadratic equation. We will be finding the zeros and vertex points to graph the quadratic. Because a > 0, the parabola opens up. And the form that it's in, it's in factored form already, it makes it pretty straightforward.
Parabola Intercept Form Definition & Explanation Video & Lesson
Web there are three major forms of linear equations: The axis of symmetry lies halfway between these points, at x = 0.5. Vertex, standard and intercept form. Identify a quadratic function written in general and vertex form. Web explore different kinds of parabolas, and learn about the standard form, the intercept form, and the vertex form of parabola equations.
4.3 Graphing Parabolas in Intercept Form Ms. Zeilstra's Math Classes
Find the equation of the line in all three forms listed above. We will be finding the zeros and vertex points to graph the quadratic. Example 1 identifying the characteristics of a parabola Web explore different kinds of parabolas, and learn about the standard form, the intercept form, and the vertex form of parabola equations. So, plug in zero for.
4.2 Graph Quadratic Functions in Vertex or Intercept Form YouTube
Web a parabola is defined as 𝑦 = 𝑎𝑥² + 𝑏𝑥 + 𝑐 for 𝑎 ≠ 0 by factoring out 𝑎 and completing the square, we get 𝑦 = 𝑎 (𝑥² + (𝑏 ∕ 𝑎)𝑥) + 𝑐 = = 𝑎 (𝑥 + 𝑏 ∕ (2𝑎))² + 𝑐 − 𝑏² ∕ (4𝑎) with ℎ = −𝑏 ∕ (2𝑎) and 𝑘 =.
How To Find X Intercepts Of A Parabola X = −b ± √b2 −4ac 2a
And the form that it's in, it's in factored form already, it makes it pretty straightforward for us to recognize when does y equal zero? Web a parabola comes from three forms of a quadratic: Find the equation of the line in all three forms listed above. Y = 12 x2 + 48 x + 49. Identify a quadratic function.
Parabola Intercept Form Definition & Explanation Video & Lesson
Given a quadratic function in general form, find the vertex. Identify a quadratic function written in general and vertex form. Notice that in this form, it is much more tedious to find various characteristics of the parabola than it is given the standard form of a parabola in the section above. Web #quadraticequation #parabola #quadratic this video shows how to.
Web The Equation Of The Parabola Is Often Given In A Number Of Different Forms.
Identify a quadratic function written in general and vertex form. We review all three in this article. Characteristics of the graph of y = a(x— + k:. Vertex, standard and intercept form.
Example 1 Identifying The Characteristics Of A Parabola
Y = 12 x2 + 48 x + 49. X = ay 2 + by + c vertex form: It fits several superficially different mathematical descriptions, which can all be proved to define exactly the same curves. The equation of a left/right opened parabola can be in one of the following three forms:
One Of The Simplest Of These Forms Is:
So, plug in zero for x and solve for y: Notice that in this form, it is much more tedious to find various characteristics of the parabola than it is given the standard form of a parabola in the section above. Web a parabola comes from three forms of a quadratic: Web a parabola is defined as 𝑦 = 𝑎𝑥² + 𝑏𝑥 + 𝑐 for 𝑎 ≠ 0 by factoring out 𝑎 and completing the square, we get 𝑦 = 𝑎 (𝑥² + (𝑏 ∕ 𝑎)𝑥) + 𝑐 = = 𝑎 (𝑥 + 𝑏 ∕ (2𝑎))² + 𝑐 − 𝑏² ∕ (4𝑎) with ℎ = −𝑏 ∕ (2𝑎) and 𝑘 = 𝑐 − 𝑏² ∕ (4𝑎) we get 𝑦 = 𝑎 (𝑥 − ℎ)² + 𝑘 (𝑥 − ℎ)² ≥ 0 for all 𝑥 so the parabola will have a vertex when (𝑥 − ℎ)² = 0 ⇔ 𝑥 = ℎ ⇒ 𝑦 = 𝑘
Web #Quadraticequation #Parabola #Quadratic This Video Shows How To Write A Quadratic Equation For A Given Graph Of A Parabola In Intercept Form.a Similar Video.
One description of a parabola involves a point (the focus) and a line (the directrix ). Web the place where the parabola crosses an axis is called an intercept. Because a > 0, the parabola opens up. Web we are graphing a quadratic equation.