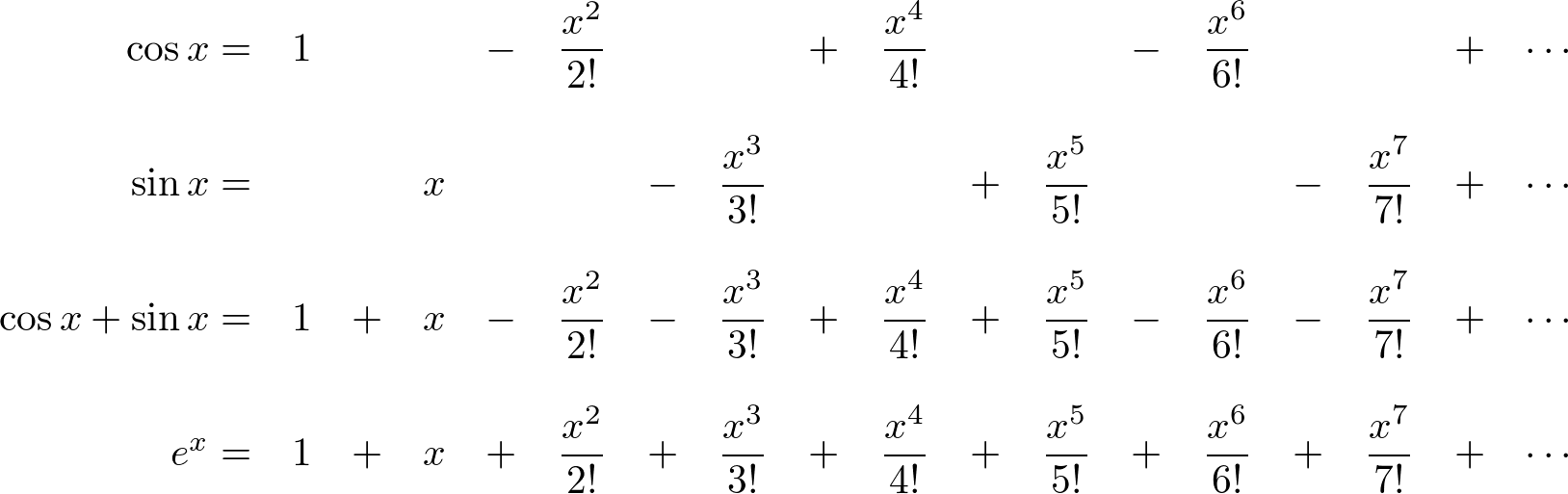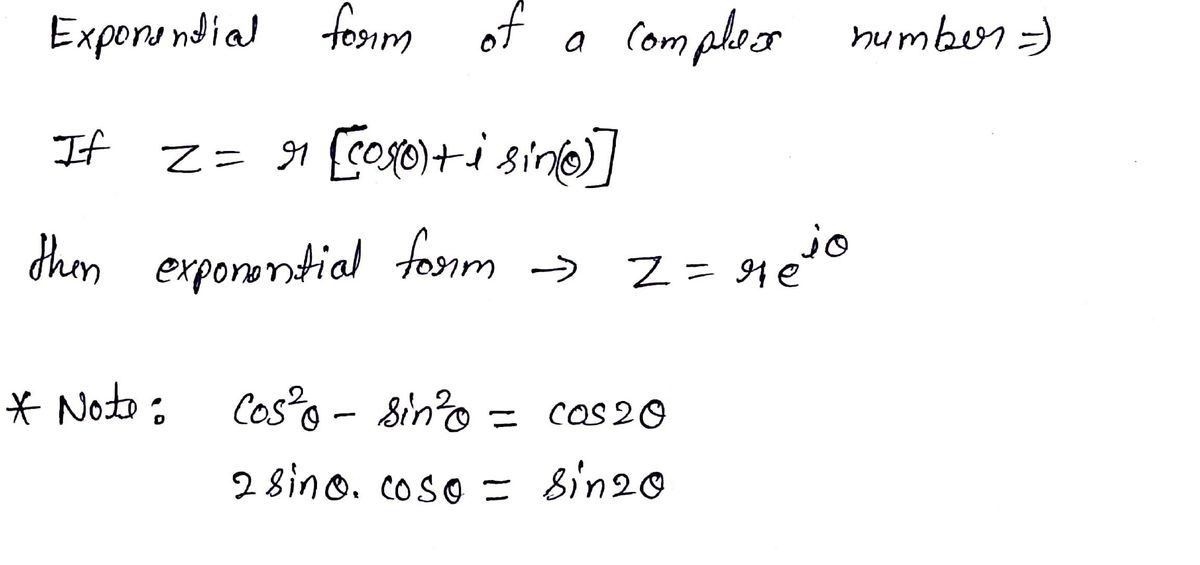Sin In Exponential Form
Sin In Exponential Form - Web according to euler, we should regard the complex exponential eit as related to the trigonometric functions cos(t) and sin(t) via the following inspired definition: Sinz = exp(iz) − exp( − iz) 2i. Periodicity of the imaginary exponential. For any complex number z : If μ r then eiμ def = cos μ + i sin μ. Web using the exponential forms of cos(theta) and sin(theta) given in (3.11a, b), prove the following trigonometric identities: Web relations between cosine, sine and exponential functions. Sin x = e i x − e − i x 2 i cos x = e i x + e − i x 2. (45) (46) (47) from these relations and the properties of exponential multiplication you can painlessly prove all. Web the exponential form of a complex number using the polar form, a complex number with modulus r and argument θ may be written = r(cos θ + j sin θ) it follows immediately from.
Web relations between cosine, sine and exponential functions. If μ r then eiμ def = cos μ + i sin μ. Periodicity of the imaginary exponential. Web solving this linear system in sine and cosine, one can express them in terms of the exponential function: Sin x = e i x − e − i x 2 i cos x = e i x + e − i x 2. I tried using eulers identity to reduce all sine. Web start with the definitions of the hyperbolic sine and cosine functions: Web spring 2003 notes on the complex exponential and sine functions (x1.5) i. (45) (46) (47) from these relations and the properties of exponential multiplication you can painlessly prove all. Web the exponential form of a complex number using the polar form, a complex number with modulus r and argument θ may be written = r(cos θ + j sin θ) it follows immediately from.
(45) (46) (47) from these relations and the properties of exponential multiplication you can painlessly prove all. Sin x = e i x − e − i x 2 i cos x = e i x + e − i x 2. Web according to euler, we should regard the complex exponential eit as related to the trigonometric functions cos(t) and sin(t) via the following inspired definition: Web relations between cosine, sine and exponential functions. E jx = cos (x) + jsin (x) and the exponential representations of sin & cos, which are derived from euler's formula: Web solving this linear system in sine and cosine, one can express them in terms of the exponential function: Sinz = exp(iz) − exp( − iz) 2i. Web using the exponential forms of cos(theta) and sin(theta) given in (3.11a, b), prove the following trigonometric identities: Expz denotes the exponential function. Sinz denotes the complex sine function.
Euler's Equation
Web an exponential equation is an equation that contains an exponential expression of the form b^x, where b is a constant (called the base) and x is a variable. Web start with the definitions of the hyperbolic sine and cosine functions: (45) (46) (47) from these relations and the properties of exponential multiplication you can painlessly prove all. Web relations.
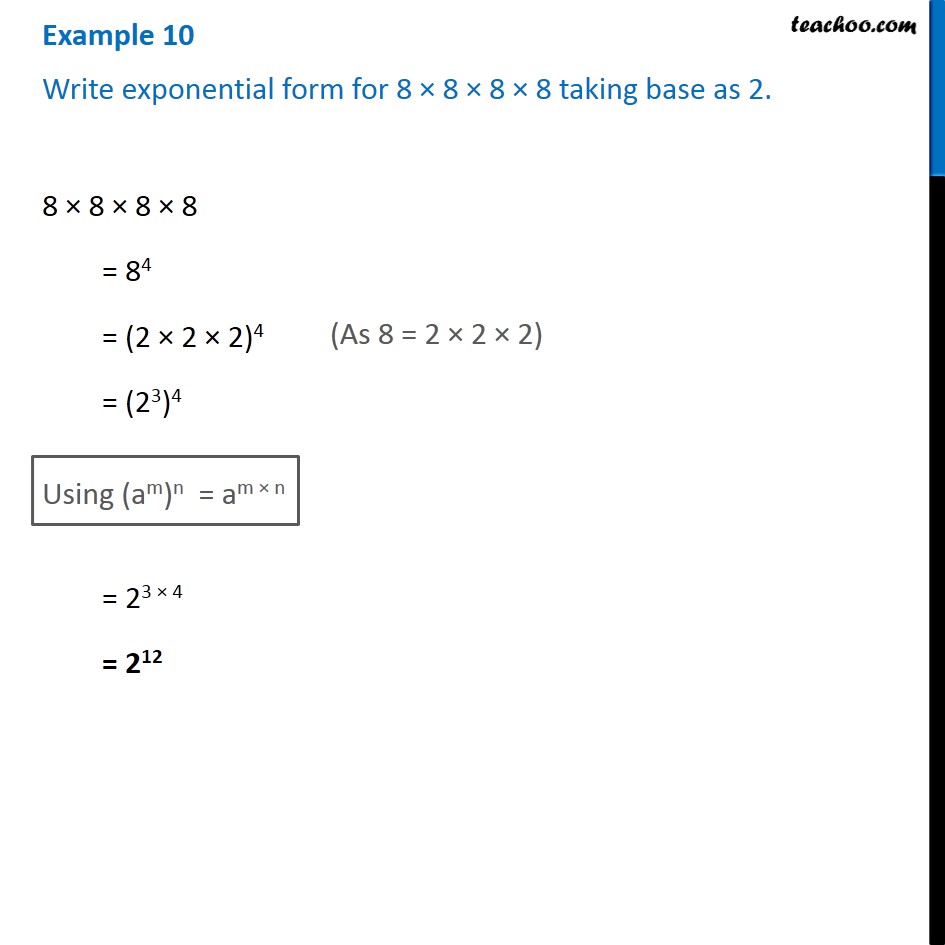
Example 10 Write exponential form for 8 x 8 x 8 x 8 taking base as 2
Sin x = e i x − e − i x 2 i cos x = e i x + e − i x 2. E jx = cos (x) + jsin (x) and the exponential representations of sin & cos, which are derived from euler's formula: Web solving this linear system in sine and cosine, one can.
voltage How to convert sine to exponential form? Electrical
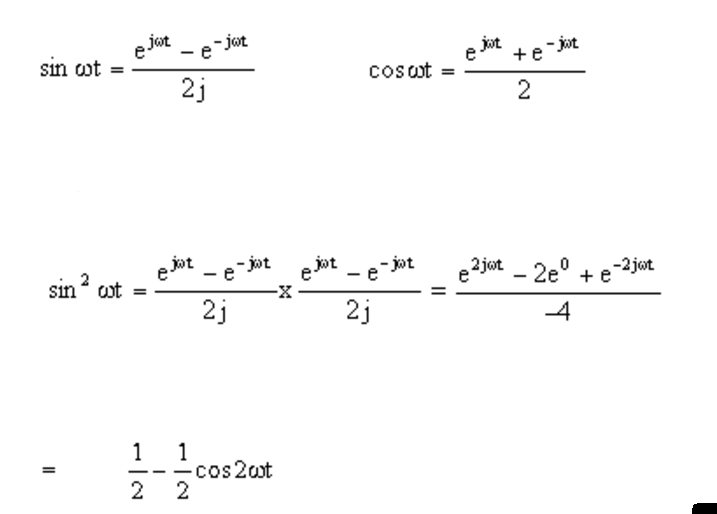
Web solving this linear system in sine and cosine, one can express them in terms of the exponential function: I tried using eulers identity to reduce all sine. A) sin(x + y) = sin(x)cos(y) + cos(x)sin(y) and. Eit = cos t + i. Web according to euler, we should regard the complex exponential eit as related to the trigonometric functions.
Question Video Converting the Product of Complex Numbers in Polar Form
Web start with the definitions of the hyperbolic sine and cosine functions: A) sin(x + y) = sin(x)cos(y) + cos(x)sin(y) and. What is going on, is that electrical engineers tend to ignore the fact that one needs to add or subtract the complex. I tried using eulers identity to reduce all sine. Web an exponential equation is an equation that.
Answered Express (cos(20)+i sin(20))*in… bartleby
Web solving this linear system in sine and cosine, one can express them in terms of the exponential function: Web an exponential equation is an equation that contains an exponential expression of the form b^x, where b is a constant (called the base) and x is a variable. Periodicity of the imaginary exponential. Web spring 2003 notes on the complex.
Basics of QPSK modulation and display of QPSK signals Electrical
Eit = cos t + i. E jx = cos (x) + jsin (x) and the exponential representations of sin & cos, which are derived from euler's formula: Web spring 2003 notes on the complex exponential and sine functions (x1.5) i. Sinz = exp(iz) − exp( − iz) 2i. Web using the exponential forms of cos(theta) and sin(theta) given in.
Exponents lesson 4 numbers in exponential form raised to a power
Web using the exponential forms of cos(theta) and sin(theta) given in (3.11a, b), prove the following trigonometric identities: Web hyperbolic functions in mathematics, hyperbolic functions are analogues of the ordinary trigonometric functions, but defined using the hyperbola rather than the circle. Periodicity of the imaginary exponential. If μ r then eiμ def = cos μ + i sin μ. Expz.
Other Math Archive January 29, 2018
Sinz denotes the complex sine function. Web start with the definitions of the hyperbolic sine and cosine functions: Sinz = exp(iz) − exp( − iz) 2i. Web the exponential form of a complex number using the polar form, a complex number with modulus r and argument θ may be written = r(cos θ + j sin θ) it follows immediately.
EM to Optics 10 Converting Cos & Sine to Complex Exponentials YouTube
For any complex number z : Sinz = exp(iz) − exp( − iz) 2i. Web according to euler, we should regard the complex exponential eit as related to the trigonometric functions cos(t) and sin(t) via the following inspired definition: Eit = cos t + i. Sin x = e i x − e − i x 2 i cos.
Particular solution for sin using complex exponentials YouTube
Web solving this linear system in sine and cosine, one can express them in terms of the exponential function: Web hyperbolic functions in mathematics, hyperbolic functions are analogues of the ordinary trigonometric functions, but defined using the hyperbola rather than the circle. Web an exponential equation is an equation that contains an exponential expression of the form b^x, where b.
Web An Exponential Equation Is An Equation That Contains An Exponential Expression Of The Form B^x, Where B Is A Constant (Called The Base) And X Is A Variable.
Web the exponential form of a complex number using the polar form, a complex number with modulus r and argument θ may be written = r(cos θ + j sin θ) it follows immediately from. What is going on, is that electrical engineers tend to ignore the fact that one needs to add or subtract the complex. Periodicity of the imaginary exponential. Web solving this linear system in sine and cosine, one can express them in terms of the exponential function:
Expz Denotes The Exponential Function.
Sin x = e i x − e − i x 2 i cos x = e i x + e − i x 2. If μ r then eiμ def = cos μ + i sin μ. For any complex number z : Sinz = exp(iz) − exp( − iz) 2i.
Web Using The Exponential Forms Of Cos(Theta) And Sin(Theta) Given In (3.11A, B), Prove The Following Trigonometric Identities:
Web spring 2003 notes on the complex exponential and sine functions (x1.5) i. (45) (46) (47) from these relations and the properties of exponential multiplication you can painlessly prove all. E jx = cos (x) + jsin (x) and the exponential representations of sin & cos, which are derived from euler's formula: Sinz denotes the complex sine function.
Eit = Cos T + I.
Web start with the definitions of the hyperbolic sine and cosine functions: Web relations between cosine, sine and exponential functions. Web according to euler, we should regard the complex exponential eit as related to the trigonometric functions cos(t) and sin(t) via the following inspired definition: A) sin(x + y) = sin(x)cos(y) + cos(x)sin(y) and.