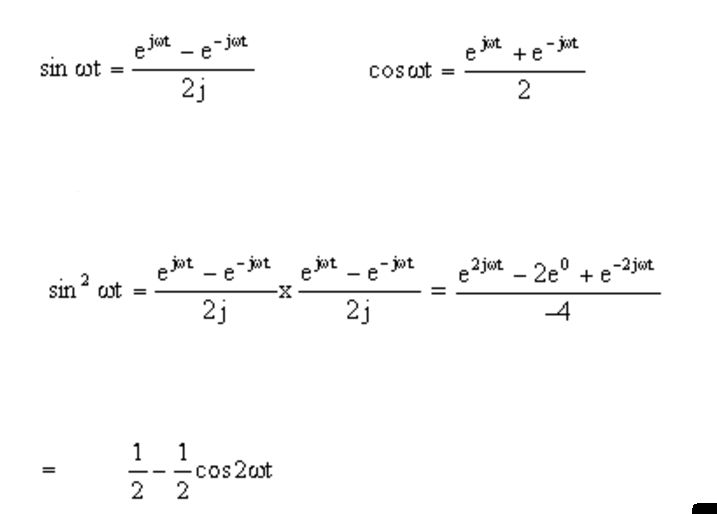
Sine And Cosine Exponential Form

Sine And Cosine Exponential Form - Web integrals of the form z cos(ax)cos(bx)dx; Using these formulas, we can derive further. As a result, the other hyperbolic functions are meromorphic in the whole complex plane. Web the hyperbolic sine and the hyperbolic cosine are entire functions. It is not currently accepting answers. Web specifically, they are the inverses of the sine, cosine, tangent, cotangent, secant, and cosecant functions, [10] and are used to obtain an angle from any of the angle's. Web euler’s formula for complex exponentials according to euler, we should regard the complex exponential eit as related to the trigonometric functions cos(t) and. By thinking of the sine and cosine values as coordinates. Web today, we derive the complex exponential definitions of the sine and cosine function, using euler's formula. Web we can use euler’s theorem to express sine and cosine in terms of the complex exponential function as s i n c o s 𝜃 = 1 2 𝑖 𝑒 − 𝑒 , 𝜃 = 1 2 𝑒 + 𝑒.

(45) (46) (47) from these relations and the properties of exponential multiplication you can painlessly prove all. This question does not appear to be about electronics design within the scope defined in. Web up to 5% cash back to represent the fourier series in concise form, the sine and cosine terms of trigonometric form, the fourier series are expressed in terms of exponential function. Fourier series coefficients are discussed for real signals. Z cos(ax)sin(bx)dx or z sin(ax)sin(bx)dx are usually done by using the addition formulas for the cosine and sine functions. Web specifically, they are the inverses of the sine, cosine, tangent, cotangent, secant, and cosecant functions, [10] and are used to obtain an angle from any of the angle's. Web the exponential form of fourier series is presented from which the sine cosine form is derived. Web today, we derive the complex exponential definitions of the sine and cosine function, using euler's formula. Y = acos(kx) + bsin(kx) according to my notes, this can also be written. Web integrals of the form z cos(ax)cos(bx)dx;

(45) (46) (47) from these relations and the properties of exponential multiplication you can painlessly prove all. Z cos(ax)sin(bx)dx or z sin(ax)sin(bx)dx are usually done by using the addition formulas for the cosine and sine functions. Web i am in the process of doing a physics problem with a differential equation that has the form: Web today, we derive the complex exponential definitions of the sine and cosine function, using euler's formula. Fourier series coefficients are discussed for real signals. As a result, the other hyperbolic functions are meromorphic in the whole complex plane. Web we can use euler’s theorem to express sine and cosine in terms of the complex exponential function as s i n c o s 𝜃 = 1 2 𝑖 𝑒 − 𝑒 , 𝜃 = 1 2 𝑒 + 𝑒. Web relations between cosine, sine and exponential functions. Web specifically, they are the inverses of the sine, cosine, tangent, cotangent, secant, and cosecant functions, [10] and are used to obtain an angle from any of the angle's. Web up to 5% cash back to represent the fourier series in concise form, the sine and cosine terms of trigonometric form, the fourier series are expressed in terms of exponential function.

Question Video Converting the Product of Complex Numbers in Polar Form

Web the hyperbolic sine and the hyperbolic cosine are entire functions. Web euler’s formula for complex exponentials according to euler, we should regard the complex exponential eit as related to the trigonometric functions cos(t) and. This question does not appear to be about electronics design within the scope defined in. Web relations between cosine, sine and exponential functions. Z cos(ax)sin(bx)dx.

Function For Sine Wave Between Two Exponential Cuves Mathematics

The sine function is one of the basic functions encountered in trigonometry (the others being the cosecant, cosine , cotangent, secant, and tangent ). Z cos(ax)sin(bx)dx or z sin(ax)sin(bx)dx are usually done by using the addition formulas for the cosine and sine functions. By thinking of the sine and cosine values as coordinates. Web we can use euler’s theorem to.

Relationship between sine, cosine and exponential function

Web today, we derive the complex exponential definitions of the sine and cosine function, using euler's formula. This question does not appear to be about electronics design within the scope defined in. Web i am in the process of doing a physics problem with a differential equation that has the form: Web the exponential form of fourier series is presented.

Other Math Archive January 29, 2018

Web conversion from exponential to cosine asked 7 years, 8 months ago modified 7 years, 8 months ago viewed 12k times 2 i'm trying to understand the following. (45) (46) (47) from these relations and the properties of exponential multiplication you can painlessly prove all. This question does not appear to be about electronics design within the scope defined in..

complex numbers Converting i to exponential form Mathematics

Web today, we derive the complex exponential definitions of the sine and cosine function, using euler's formula. Web specifically, they are the inverses of the sine, cosine, tangent, cotangent, secant, and cosecant functions, [10] and are used to obtain an angle from any of the angle's. By thinking of the sine and cosine values as coordinates. Web relations between cosine,.

Basics of QPSK modulation and display of QPSK signals Electrical

This question does not appear to be about electronics design within the scope defined in. Web conversion from exponential to cosine asked 7 years, 8 months ago modified 7 years, 8 months ago viewed 12k times 2 i'm trying to understand the following. Web up to 5% cash back to represent the fourier series in concise form, the sine and.

EM to Optics 10 Converting Cos & Sine to Complex Exponentials YouTube

Web up to 5% cash back to represent the fourier series in concise form, the sine and cosine terms of trigonometric form, the fourier series are expressed in terms of exponential function. (45) (46) (47) from these relations and the properties of exponential multiplication you can painlessly prove all. Web the hyperbolic sine and the hyperbolic cosine are entire functions..

PPT Graphing Sine and Cosine Functions PowerPoint Presentation, free

Web integrals of the form z cos(ax)cos(bx)dx; Web the hyperbolic sine and the hyperbolic cosine are entire functions. By thinking of the sine and cosine values as coordinates. Web today, we derive the complex exponential definitions of the sine and cosine function, using euler's formula. Web because we can evaluate the sine and cosine of any real number, both of.

Write Equations Of Sine Functions Using Properties Calculator

It is not currently accepting answers. Z cos(ax)sin(bx)dx or z sin(ax)sin(bx)dx are usually done by using the addition formulas for the cosine and sine functions. Web relations between cosine, sine and exponential functions. By thinking of the sine and cosine values as coordinates. Web we can use euler’s theorem to express sine and cosine in terms of the complex exponential.

Sine and cosine problems Math Tutoring & Exercises

By thinking of the sine and cosine values as coordinates. Using these formulas, we can derive further. Web the exponential form of fourier series is presented from which the sine cosine form is derived. Web up to 5% cash back to represent the fourier series in concise form, the sine and cosine terms of trigonometric form, the fourier series are.

It Is Not Currently Accepting Answers.

Web up to 5% cash back to represent the fourier series in concise form, the sine and cosine terms of trigonometric form, the fourier series are expressed in terms of exponential function. By thinking of the sine and cosine values as coordinates. Web today, we derive the complex exponential definitions of the sine and cosine function, using euler's formula. Web relations between cosine, sine and exponential functions.

The Sine Function Is One Of The Basic Functions Encountered In Trigonometry (The Others Being The Cosecant, Cosine , Cotangent, Secant, And Tangent ).

Using these formulas, we can derive further. Web euler’s formula for complex exponentials according to euler, we should regard the complex exponential eit as related to the trigonometric functions cos(t) and. Web specifically, they are the inverses of the sine, cosine, tangent, cotangent, secant, and cosecant functions, [10] and are used to obtain an angle from any of the angle's. Web because we can evaluate the sine and cosine of any real number, both of these functions are defined for all real numbers.

(45) (46) (47) From These Relations And The Properties Of Exponential Multiplication You Can Painlessly Prove All.

Web integrals of the form z cos(ax)cos(bx)dx; Web i am in the process of doing a physics problem with a differential equation that has the form: Let be an angle measured. Web we can use euler’s theorem to express sine and cosine in terms of the complex exponential function as s i n c o s 𝜃 = 1 2 𝑖 𝑒 − 𝑒 , 𝜃 = 1 2 𝑒 + 𝑒.

As A Result, The Other Hyperbolic Functions Are Meromorphic In The Whole Complex Plane.

Web the hyperbolic sine and the hyperbolic cosine are entire functions. Web the exponential form of fourier series is presented from which the sine cosine form is derived. Y = acos(kx) + bsin(kx) according to my notes, this can also be written. This question does not appear to be about electronics design within the scope defined in.